I recently put together a Bluetooth audio receiver as a weekend project. At some point I got to the point of regulating the volume and had to realize that it is not that easy to do it well. As always, I researched the Internet for a while, in the end I had to experiment myself, true to the motto that you can’t program anything sensible that you don’t understand.
Volume and hearing
Our ear is an impressive organ. The audible range from the softest sound to the greatest noise spans about 6 decades. This means that the slightest sound is a million times quieter than the loudest we can hear. Since there is no physical upper limit for noise, the volume of hearing is set as the maximum, which we can hear for a short time without permanent damage.
Another important fact is that we can differentiate quieter sounds much better in terms of volume. This is noticeable in the fact that we can hear differences in volume very well with soft tones. The louder it gets, the less we notice a change.
This results in the following requirements for a good volume control: In the quiet area you have to be able to set very precisely in very small steps. The louder it gets, the bigger the steps and the change.
Of course, this was already known almost 100 years ago, and volume controls or potentiometers with a so-called logarithmic curve are built into even ancient analog electronics. On old potentiometers, for example, there is still “100kΩ log” for 100 kiloohms with a logarithmic course or e.g. “1M lin” for 1 megaohm and a linear course. On current models, the gradient is usually identified with the first letter:
-
- “A20k” corresponds logarithmically, 20kΩ
- “B2k” means linear 2kΩ
- “C50k” means anti-logarithmic 50kΩ
With the advent of digital technology, however, some engineers did not do their homework and there are many (digital) devices in which the volume control does not work properly. Often the gradation in the lower range is too coarse, sometimes there are too few levels with 32 or even fewer setting levels.
Comparison of different functions
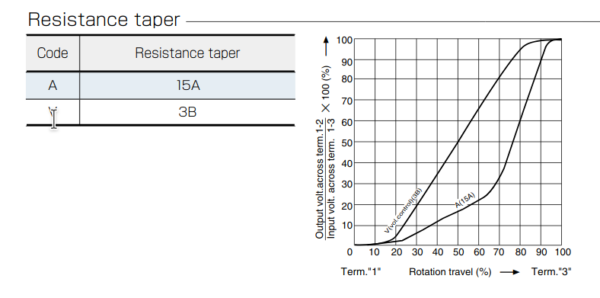
As far as I know, a logarithmic curve for a volume control or a potentiometer is not exactly mathematically defined. According to the data sheets of some manufacturers, the resistance curves are partly linear with smooth transitions. For example, a manufacturer of high-quality audio potentiometers (Alps Alpine) has a curve with three linear ranges; flat up to almost 25%, a little steeper up to 65% and very steep at more than 65% angle of rotation.
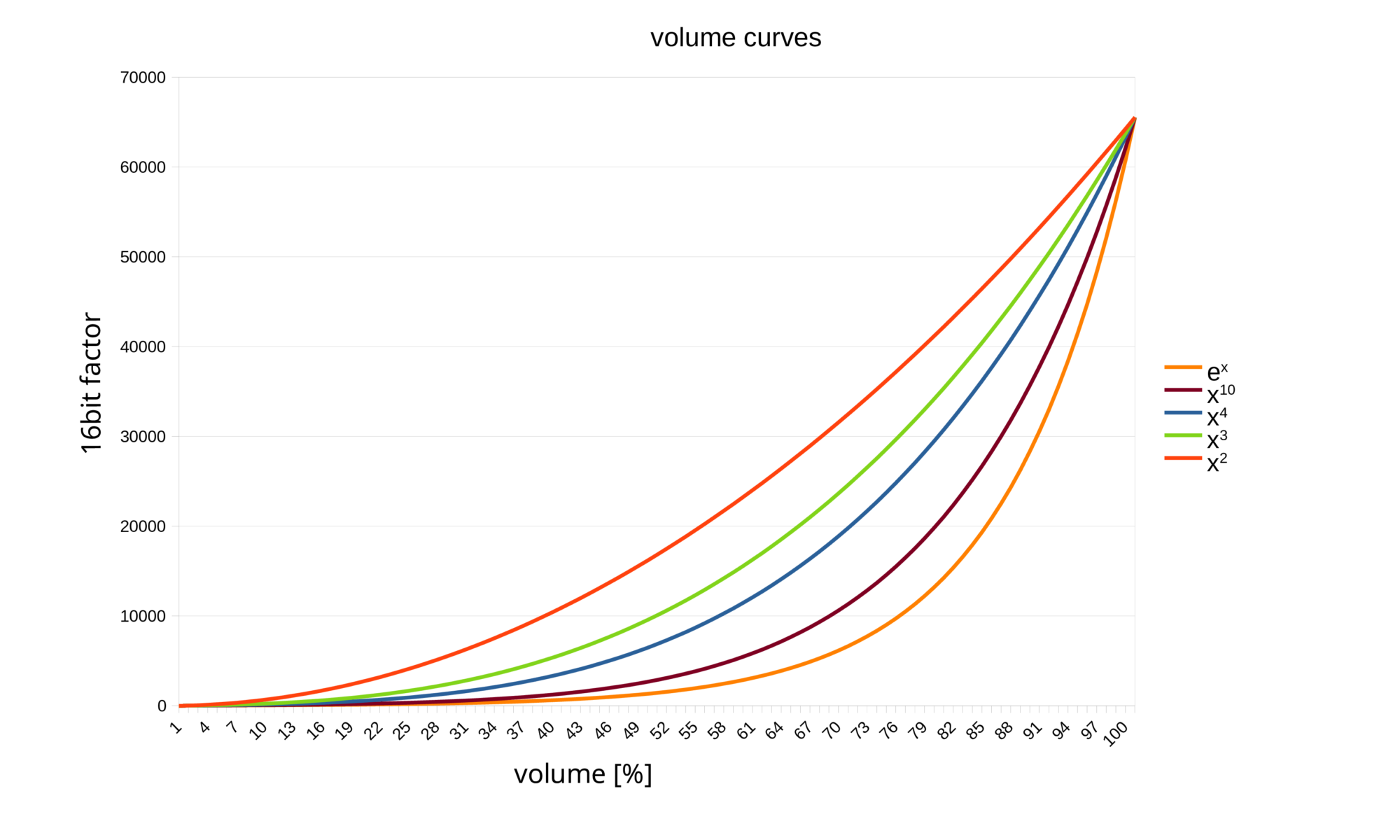
One could of course relate to this digitally, but that would be relatively time-consuming. A math function is of course much easier to program.
The desired curve shape, i.e. flat at the beginning, steep at the end, follows more of an exponential function or power functions. The higher the potency, the flatter the rise in the lower area and the steeper at the end. I tried different functions, first displayed the curves, then tested them by ear.
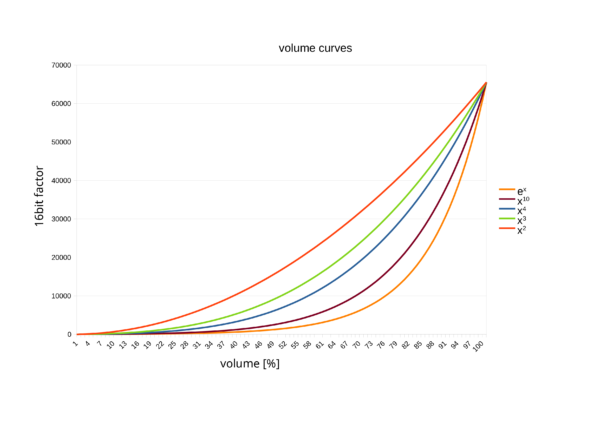
Optimal function
Judging by my ear, the function y = x³ has proven to be optimal. I also add a small offset so that the regulation begins in the lower range around the hearing threshold.
Calculation of the volume
To regulate the volume of digital audio data, a factor is normally used by which each audio sample is multiplied. If you work with floating point numbers, the factor is usually between 0 and 1. With fixed point arithmetic, the factor can be completely different. In the following an example as a C code, where the volume factor is a 16 bit value between 0 and 65536 and is calculated with the function y = x³.
If you multiply this value by 16-bit audio samples, you get 32-bit values as the result. I use this in a Bluetooth receiver, where 16-bit audio is received via Bluetooth and, after volume calculation, is output to a 32-bit PCM5102A D / A converter without loss of quality.
#include <stdint.h>
#include <stdlib.h>
#include <math.h>
//use x^3 function
#define VOL_POWER 3.0
//upper/lower limit of factor to multiply with samples
#define VOL_MIN 30.0
#define VOL_MAX 65536.0
//precalculate constants once
static const float vol_pow_min = pow(VOL_MIN, (1.0 / VOL_POWER));
static const float vol_pow_diff = pow(VOL_MAX, (1.0 / VOL_POWER)) - pow(VOL_MIN, (1.0 / VOL_POWER));
//calculate volume factor with power function
//argument vol: 0..100%
static uint32_t vol_calc(uint8_t vol) {
if (vol == 0) return 0;
if (vol >= 100) return VOL_MAX;
return floor(pow((vol_pow_min + vol_pow_diff / 100 * vol), VOL_POWER));
}
As a little calculation aid and for your own experiments, my table with the series of numbers and experiments can be downloaded here: volume_calc.ods