Kürzlich habe ich als Wochenendprojekt einen Bluetooth Audio Empfänger zusammengebastelt. Dabei kam ich irgendwann an den Punkt, die Lautstärke zu regulieren und musste feststellen, dass es gar nicht so einfach ist, das gut zu machen. Ich habe wie immer eine Weile im Internet recherchiert, am Ende musste ich selbst experimentieren getreu dem Motto, dass man nichts vernünftig programmieren kann, was man nicht versteht.
Lautstärke und Gehör
Unser Ohr ist ein eindrucksvolles Organ. Der Hörbereich vom leisestem Ton bis zum größten Krach umfasst etwa 6 Dekaden. Das bedeutet, dass das leiseste Geräusch eine Million mal leiser ist als das lauteste, was wir wahrnehmen können. Da es bei Lärm physikalisch keine Obergrenze gibt, wird beim Gehör die Lautstärke als Maximum festgelegt, welche wir kurzzeitig ohne bleibenden Schaden hören können.
Ein weiterer wichtiger Fakt ist, dass wir leisere Töne viel besser in der Lautstärke differenzieren können. Das macht sich daran bemerkbar, dass wir bei leisen Tönen sehr gut Unterschiede in der Lautstärke hören. Je lauter es wird, umso weniger bemerken wir eine Veränderung.
Daraus ergeben sich folgende Forderungen an eine gute Lautstärkeregelung: Im leisen Bereich muss man in sehr kleinen Schritten sehr genau einstellen können. Je lauter es wird, umso größer werden Schritte und Änderung.
Das hat man natürlich auch schon vor fast 100 Jahren gewusst und selbst in uralter Analogelektronik sind Lautstärkeregler bzw. Potentiometer mit sogenanntem logarithmischen Verlauf eingebaut. Auf alten Potentiometern steht z.B. noch „100kΩ log“ für 100 Kiloohm mit logarithmischen Verlauf oder z.B. „1M lin“ für 1 Megaohm und linearen Verlauf. Auf aktuellen Modellen wird normalerweise der Verlauf mit dem ersten Buchstaben gekennzeichnet:
-
- „A20k“ entspricht logarithmisch, 20kΩ
- „B2k“ bedeutet linear 2kΩ
- „C50k“ heißt anti-logarithmisch 50kΩ
Mit Einzug der Digitaltechnik haben einige Ingenieure aber nicht ihre Hausaufgaben gemacht und es gibt viele (digitale) Geräte, in denen die Lautstärkeregelung mangelhaft funktioniert. Oft ist die Abstufung im unteren Bereich zu grob, manchmal sind es zu wenige Stufen mit 32 oder noch weniger Einstellstufen.
Vergleich verschiedener Funktionen
Ein logarithmischer Verlauf bei einer Lautstärkeregelung bzw. einem Potentiometer ist meines Wissens nach gar nicht exakt mathematisch definiert. Den Datenblättern einiger Hersteller nach zu urteilen sind die Widerstandsverläufe zum Teil linear mit sanften Übergängen. Ein Hersteller für hochwertige Audio-Potentiometer (Alps Alpine) hat z.B. einen Verlauf mit drei linearen Bereichen; flach bis knapp 25%, etwas steiler bis 65% und sehr steil bei mehr als 65% Drehwinkel.
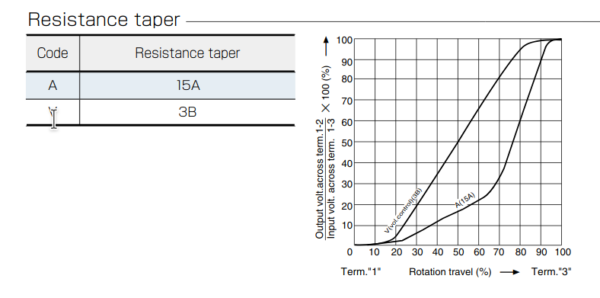
Das könnte man natürlich digital nachempfinden, was aber relativ aufwändig wäre. Eine mathematische Funktion ist natürlich viel einfacher zu programmieren.
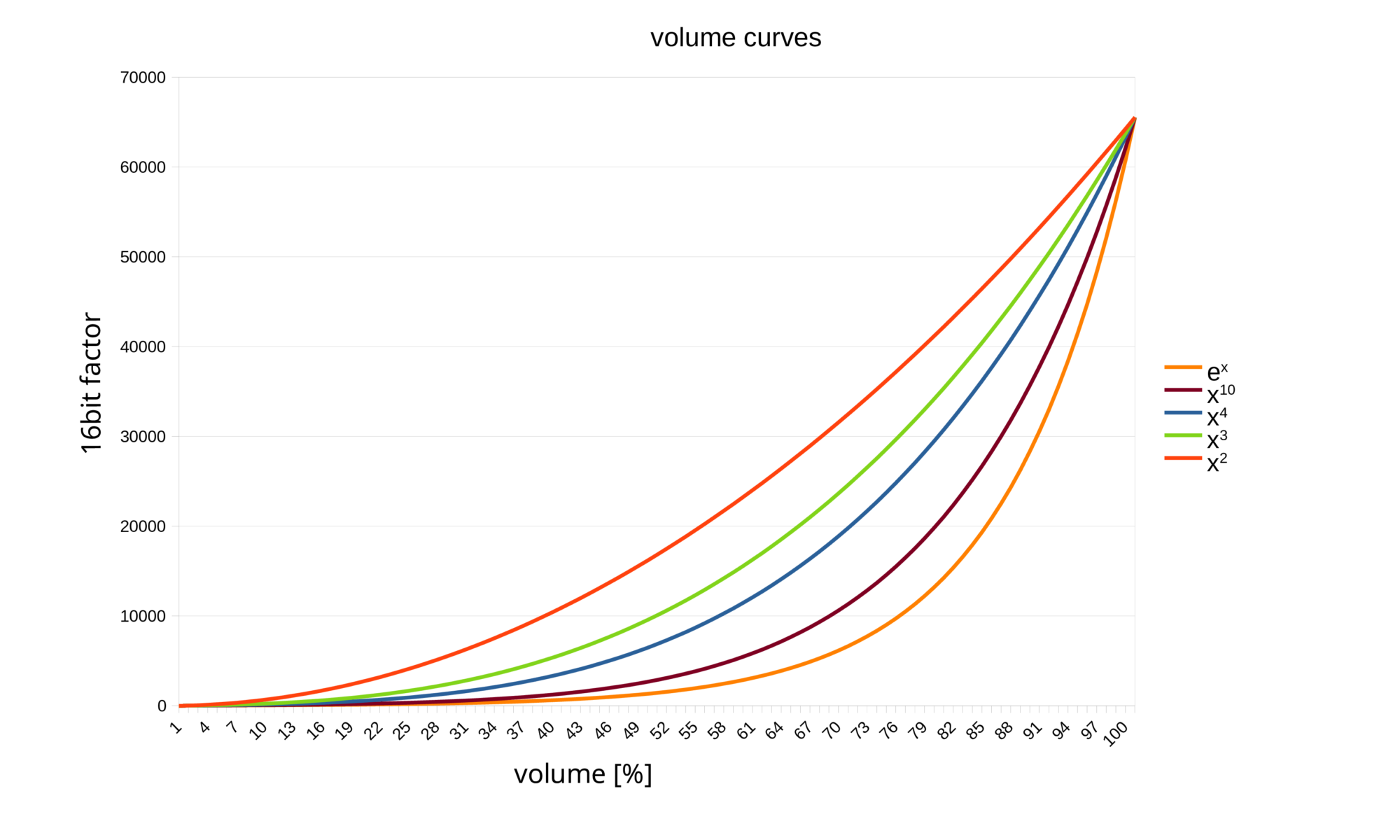
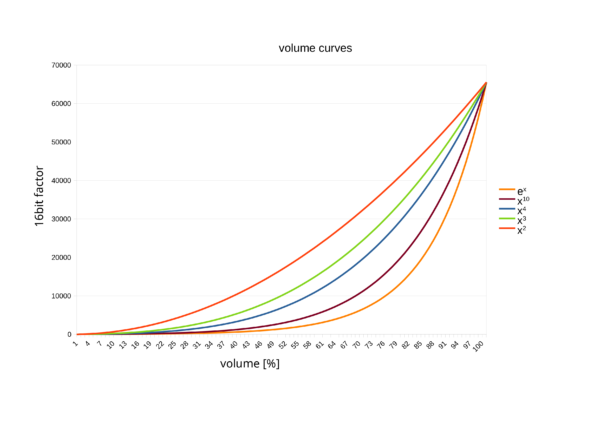
Der gewünschte Kurvenverlauf, also Anfangs flach, am Ende steil, folgt ja eher einer Exponentialfunktion oder Potenzfunktionen. Je höher die Potenz, umso flacher der Anstieg im unteren Bereich und umso steiler am Ende. Ich habe verschiedene Funktionen ausprobiert, zunächst die Kurven dargestellt, danach per Gehör getestet.
Optimale Funktion
Nach meinem Gehör beurteilt hat sich die Funktion y=x³ als optimal herausgestellt. Dabei addiere ich noch einen kleinen Offset, damit die Regelung im unteren Bereich etwa bei der Hörschwelle beginnt.
Berechnung der Lautstärke
Für die Regulierung der Lautstärke wird bei digitalen Audiodaten normalerweise ein Faktor benutzt, mit dem jedes Audio-Sample multipliziert wird. Falls man mit Fließkommazahlen arbeitet, liegt der Faktor üblicherweise zwischen 0 und 1. Bei Festpunktarithmetik kann der Faktor ganz unterschiedlich sein. Im Folgenden ein Beispiel als C-Code, wo der Lautstärkefaktor ein 16 Bit Wert zwischen 0 und 65536 ist und mit der Funktion y=x³ errechnet wird.
Wenn man diesen Wert nun mit 16 Bit Audio Samples multipliziert, bekommt man 32 Bit Werte als Ergebnis. Ich verwende das so in einem Bluetooth-Empfänger, wo 16 Bit Audio über Bluetooth empfangen wird und nach Lautstärkeberechnung ohne Qualitätsverlust an einen 32 Bit D/A-Wandler PCM5102A ausgegeben wird.
#include <stdint.h>
#include <stdlib.h>
#include <math.h>
//use x^3 function
#define VOL_POWER 3.0
//upper/lower limit of factor to multiply with samples
#define VOL_MIN 30.0
#define VOL_MAX 65536.0
//precalculate constants once
static const float vol_pow_min = pow(VOL_MIN, (1.0 / VOL_POWER));
static const float vol_pow_diff = pow(VOL_MAX, (1.0 / VOL_POWER)) - pow(VOL_MIN, (1.0 / VOL_POWER));
//calculate volume factor with power function
//argument vol: 0..100%
static uint32_t vol_calc(uint8_t vol) {
if (vol == 0) return 0;
if (vol >= 100) return VOL_MAX;
return floor(pow((vol_pow_min + vol_pow_diff / 100 * vol), VOL_POWER));
}
Als kleine Berechnungshilfe und für eigene Experimante kann hier noch meine Tabelle mit den Zahlenreihen und Versuchen heruntergeladen werden: volume_calc.ods